
|
I N G E G N E R E ONDA TROCOIDALE |

|
I N G E G N E R E ONDA TROCOIDALE |
In alcune applicazioni dell'architettura navale viene usata l'onda di Gerstner (onda trocoidale) che è una buona approssimazione dell'onda marina (fondale infinito). È la soluzione matematica (bidimensionale e stazionaria) in cui la condizione di superficie libera viene assolta esattamente (forse l'unico caso) come pure la conservazione della massa [div(v) = 0] ma il flusso ha una seppur piccola componente rotazionale [|rot(v)| > 0]. Le particelle d'acqua descrivono traiettorie circolari il cui raggio decresce esponenzialmente con l'immersione.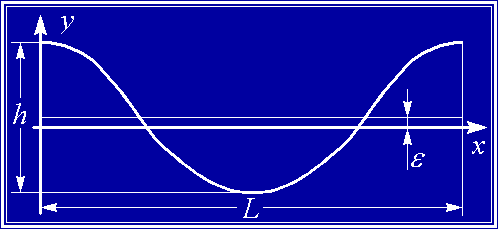
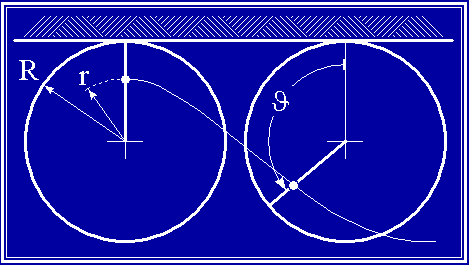
Il profilo di tale onda risulta una trocoide cioè la curva che corrisponde alla traiettoria di un punto interno di un cerchio che viene fatto rotolare lungo una retta orizzontale posta al di sopra del cerchio stesso (la costante di compenso e è stata introdotta per far sí che l'arê al di sopra ed al di sotto dell'asse x siano uguali)
 h = Altezza dell'onda dal cavo alla cresta
h = Altezza dell'onda dal cavo alla cresta
L = Lunghezza dell'onda
R = L : (2 p)
r = h : 2
e = r2 : (2 R)x = RJ - r sen(J)
y = r cos(J) + eUna complicazione nell'uso dell'onda di Gerstner è l'impossibilità di esprimere l'altezza y con una funzione sempice (cioé una composizione di funzioni note) di x. Si può ovviare a questo inconveniente utilizzando onde a profilo sinusoidale che, nelle applicazioni pratiche, spesso danno risultati che si discostano pochissimo da quelli ottenuti con onde a profilo trocoidale oppure si può calcolare il profilo dell'onda trocoidale con uno dei metodi di seguito esposti.
APPROSSIMAZIONE CON UNA SERIE MISTA
È possibile esprimere la trocoinde in funzione di x con una serie di Fourier dei soli coseni i cui coefficienti a sono calcolabili , in funzione del rapporto h:L, con un polinomio determinato con il metodo dei minimi quadrati.
Nella pratica si ottengono ottime approssimazioni troncando sia la serie che il polinomio al ternine di quart'ordine (formule e tabelle sottostanti). Gli errori massimi relativi ad h, più che accettabili nei casi reali, sono: 0,02% per L:h = 40, 0,03% per L:h = 30, 0,04% per L:h = 20, 0,07% per L:h = 15, 0,25% per L:h = 10, 3,65% per L:h = 5.
r = h : L
l = 2 p : Lan = b0n + b1n r + b2n r2 + b3n r3 + b4n r4
y = h [ a1 cos(l x) + a2 cos(2 l x) + a3 cos(3 l x) + a4 cos(4 l x) ]
n=1 n=2 n=3 n=4 b0n b1n b2n b3n b4n
ALGORITMO ITERATIVO
Con l'utilizzo di questo algoritmo è possibile calcolare l'altezza y in ogni punto x con la voluta precisione. Nel caso dell'utilizzo del calcolatore è opportuno inserire il controllo che sia L:H>p e non assegnare d cosí piccolo da correre il rischio che gli errori di macchina gli siano maggiori (si rischia che il ciclo non termini mai). Si noti che, per come è stato scritto, l'algoritmo fornisce un risultato molto più precisa del richiesto; non sarebbe difficile rendere la condizione di fine ciclo più fine ma, in considerazione della potenza degli attuali mezzi di calcolo, sarebbe una complicazione inutile.
1. ASSEGNAZIONE DATI L = lunghezza dell'onda h = altezza dell'onda d = errore ammissibile (assoluto) X = ascissa in corrispondenza della quale calcolre l'altezza y 2. CALCOLO PARAMETRI R = L : (2 p) r = h : 2 e = r2 : (2 R) s = 0,5 (costante di sottorilassamento; dev'essere s<=1 per la stabilità dell'algoritmo) 3. PREASSEGNAZIONE J = x:R 4. CALCOLO PARAMETRI FALSA POSIZIONE x = RJ - r sen(J) x' = R - r cos(J) D = (X - x) Q = D : x' 5. AGGIORNAMENTO J = J + s Q 6. VERIFICA Se |D| > d torna al punto 4 7. CALCOLO DI y y = r cos(J) + e 8. FINE
![]()